二叉树数组表示

在链表表示下，二叉树的存储单元为节点 TreeNode ，节点之间通过指针相连接。上一节介绍了链表表示下的二叉树的各项基本操作。

那么，我们能否用数组来表示二叉树呢？答案是肯定的。

表示完美二叉树

先分析一个简单案例。给定一棵完美二叉树，我们将所有节点按照层序遍历的顺序存储在一个数组中，则每个节点都对应唯一的数组索引。

根据层序遍历的特性，我们可以推导出父节点索引与子节点索引之间的“映射公式”：若某节点的索引为 i ，则该节点的左子节点索引为 2i + 1 ，右子节点索引为 2i + 2 。下图展示了各个节点索引之间的映射关系。

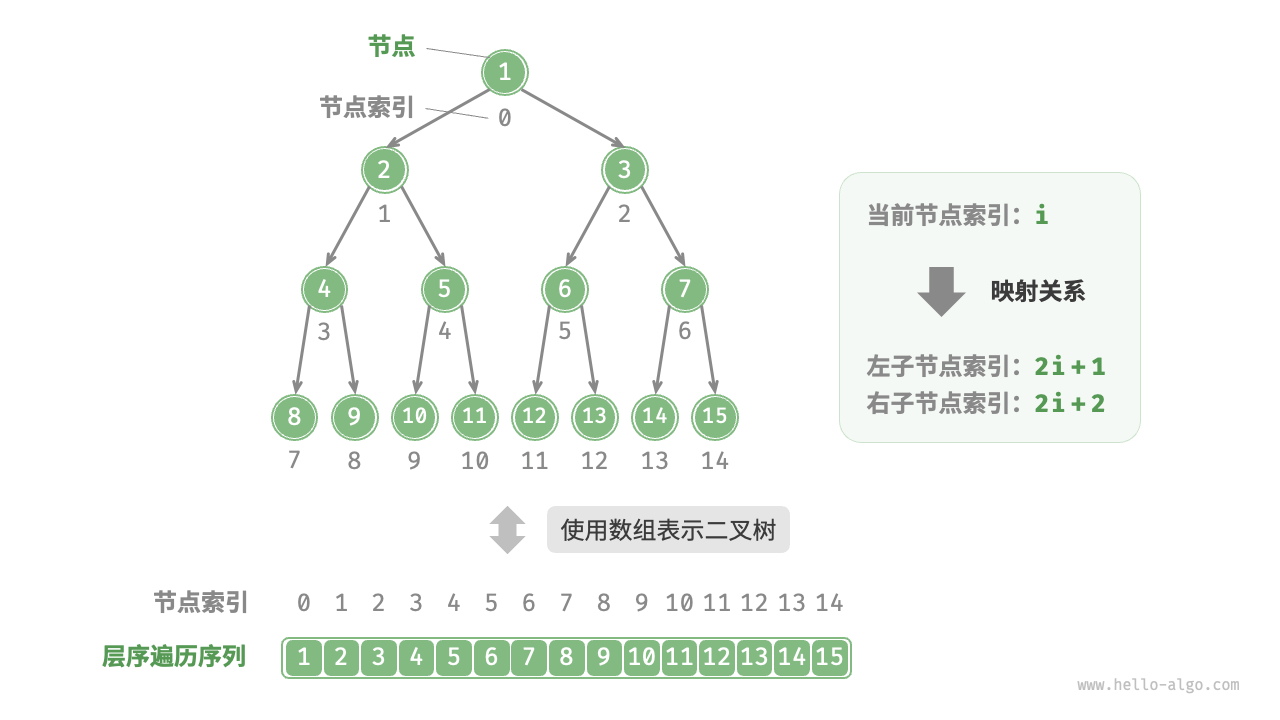
映射公式的角色相当于链表中的节点引用（指针）。给定数组中的任意一个节点，我们都可以通过映射公式来访问它的左（右）子节点。

表示任意二叉树

完美二叉树是一个特例，在二叉树的中间层通常存在许多 None 。由于层序遍历序列并不包含这些 None ，因此我们无法仅凭该序列来推测 None 的数量和分布位置。这意味着存在多种二叉树结构都符合该层序遍历序列。

如下图所示，给定一棵非完美二叉树，上述数组表示方法已经失效。

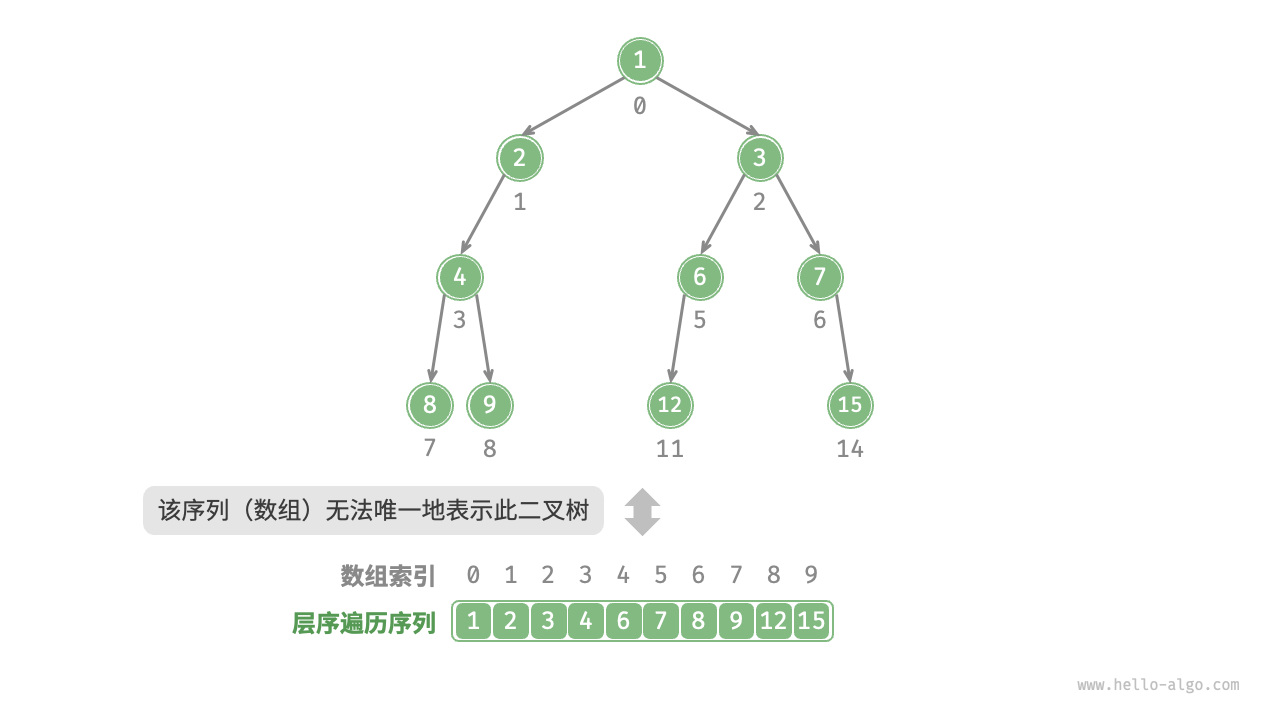
为了解决此问题，我们可以考虑在层序遍历序列中显式地写出所有 None 。如下图所示，这样处理后，层序遍历序列就可以唯一表示二叉树了。示例代码如下：

/* 二叉树的数组表示 */
// 使用 int 的包装类 Integer ，就可以使用 null 来标记空位
Integer[] tree = { 1, 2, 3, 4, null, 6, 7, 8, 9, null, null, 12, null, null, 15 };

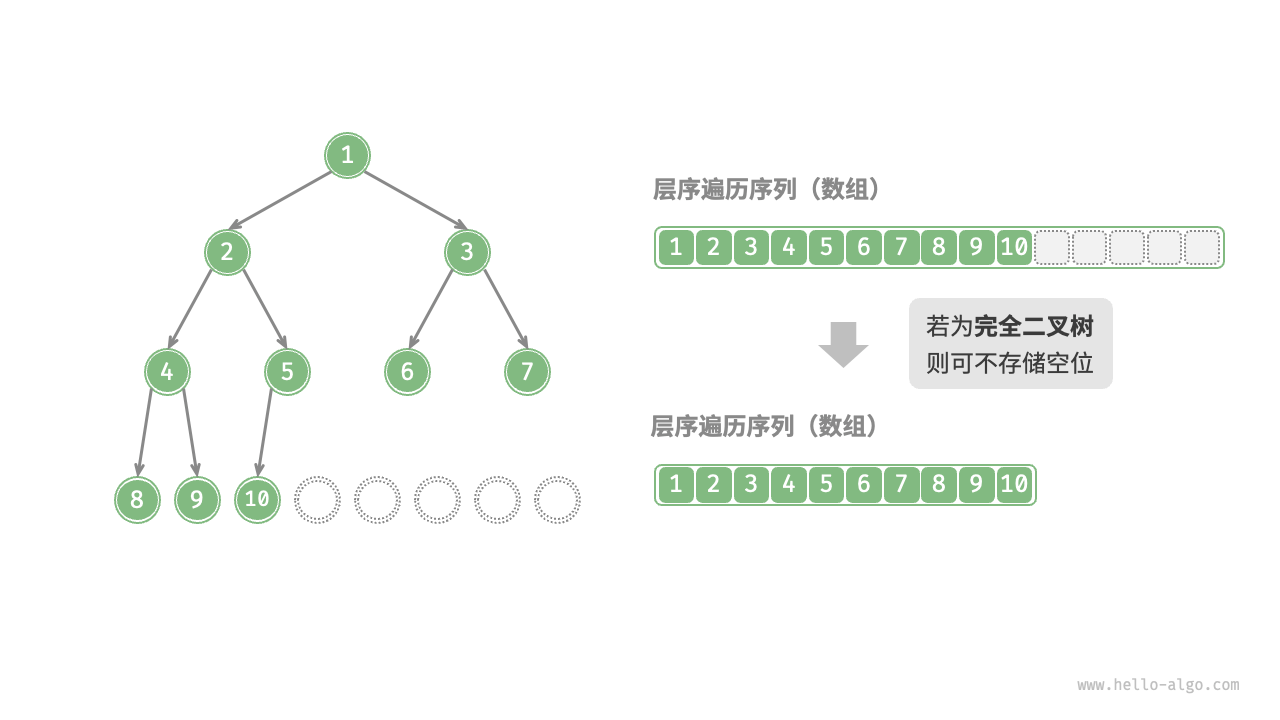
值得说明的是，完全二叉树非常适合使用数组来表示。回顾完全二叉树的定义，None 只出现在最底层且靠右的位置，因此所有 None 一定出现在层序遍历序列的末尾。

这意味着使用数组表示完全二叉树时，可以省略存储所有 None ，非常方便。下图给出了一个例子。

以下代码实现了一棵基于数组表示的二叉树，包括以下几种操作。

• 给定某节点，获取它的值、左（右）子节点、父节点。
• 获取前序遍历、中序遍历、后序遍历、层序遍历序列。

/* 数组表示下的二叉树类 */
class ArrayBinaryTree {
    private List<Integer> tree;

    /* 构造方法 */
    public ArrayBinaryTree(List<Integer> arr) {
        tree = new ArrayList<>(arr);
    }

    /* 列表容量 */
    public int size() {
        return tree.size();
    }

    /* 获取索引为 i 节点的值 */
    public Integer val(int i) {
        // 若索引越界，则返回 null ，代表空位
        if (i < 0 || i >= size())
            return null;
        return tree.get(i);
    }

    /* 获取索引为 i 节点的左子节点的索引 */
    public Integer left(int i) {
        return 2 * i + 1;
    }

    /* 获取索引为 i 节点的右子节点的索引 */
    public Integer right(int i) {
        return 2 * i + 2;
    }

    /* 获取索引为 i 节点的父节点的索引 */
    public Integer parent(int i) {
        return (i - 1) / 2;
    }

    /* 层序遍历 */
    public List<Integer> levelOrder() {
        List<Integer> res = new ArrayList<>();
        // 直接遍历数组
        for (int i = 0; i < size(); i++) {
            if (val(i) != null)
                res.add(val(i));
        }
        return res;
    }

    /* 深度优先遍历 */
    private void dfs(Integer i, String order, List<Integer> res) {
        // 若为空位，则返回
        if (val(i) == null)
            return;
        // 前序遍历
        if ("pre".equals(order))
            res.add(val(i));
        dfs(left(i), order, res);
        // 中序遍历
        if ("in".equals(order))
            res.add(val(i));
        dfs(right(i), order, res);
        // 后序遍历
        if ("post".equals(order))
            res.add(val(i));
    }

    /* 前序遍历 */
    public List<Integer> preOrder() {
        List<Integer> res = new ArrayList<>();
        dfs(0, "pre", res);
        return res;
    }

    /* 中序遍历 */
    public List<Integer> inOrder() {
        List<Integer> res = new ArrayList<>();
        dfs(0, "in", res);
        return res;
    }

    /* 后序遍历 */
    public List<Integer> postOrder() {
        List<Integer> res = new ArrayList<>();
        dfs(0, "post", res);
        return res;
    }
}

优点与局限性

二叉树的数组表示主要有以下优点。

• 数组存储在连续的内存空间中，对缓存友好，访问与遍历速度较快。
• 不需要存储指针，比较节省空间。
• 允许随机访问节点。

然而，数组表示也存在一些局限性。

• 数组存储需要连续内存空间，因此不适合存储数据量过大的树。
• 增删节点需要通过数组插入与删除操作实现，效率较低。
• 当二叉树中存在大量 None 时，数组中包含的节点数据比重较低，空间利用率较低。