加盐?

盐又称为Salt，在密码学中我们常常会用到散列算法对字符串进行处理，散列算法可以为数据创建相对精简的数据指纹，具体我们会在后面详细介绍。为了提高安全性，在进行散列操作之前会对字符串进行一些拼接、混淆操作，这个过程我们就称为“加盐”。虽然不知道“加盐”的本意是否如此，但加盐处理字符串的过程与使用盐处理食物的过程非常相似，一方面去除了字符串本身的特征，另一方面增强了字符串的复杂度。

经过加盐处理的散列结果与未加盐处理的散列结果，极大概率是不相同的，这一过程大大提高了散列算法的安全性。

原材料 Hash

HASH函数，又称散列函数，是为一段数据创建数字指纹的方法，创建生成的数字指纹叫散列值。由于经过了压缩，它的长度较原始输入短了很多，因此我们也称之为摘要。

由HASH函数计算出来的散列值具有不可逆的特性，这里说的不可逆，是指攻击者无法从散列值进行逆向推导，进而获得原始输入。得益于不可逆特性，在Web业务系统开发过程中，我们通常使用散列值作为用户密码存储进数据库。在这种情况下，Web业务系统既可以校验用户密码的正确性，又无法真正得知用户密码明文。

主要应用场景

我们都知道，密码的存储通常是放在数据库中，关于密码的存储形态有很多种，通常可选的方案包括明文、散列值等。

如果采用明文存储的方案，一旦发生了入侵事件，或者系统存在漏洞使得数据库外泄，就会导致大规模的用户账户外泄，这种安全事件是灾难性的。所以目前大部分系统采取的方案都是存储散列值，在这种情况下，即使是系统也无法得知用户的密码是什么。

通常在采用存储散列值的情况下，系统会通过比较散列值来认证用户。系统通过用户输入获得密码后，会让密码经过HASH函数处理产生一个散列值，并将该散列值与存储在数据库中的散列值进行对比，如果相同则表示认证成功。

我们可以设想一下，在这种方案下，即使黑客通过漏洞成功获得了数据库内的全部数据，他获得的，也仅仅是密码经过HASH函数运算得出的散列值，而这个散列值并不能够帮助他登录系统。

暴力破解和字典攻击

为了达到登录的目的，黑客必须找到一段数据，这段数据的HASH运算结果需要与黑客获得的散列值一致。此时黑客可选的方案是暴力破解、字典攻击和彩虹表攻击。

这三种攻击方式执行的难度由简单到困难，效果也是从差到好。暴力破解和字典攻击的实施过程都非常简单，**基本思路都是通过遍历用户密码所有取值来直接找到答案，区别是暴力破解采用遍历的方式是实时计算，而字典攻击会根据预先计算好的结果直接查找。**虽然这两种方案执行上非常简单，但实际操作效果却并不理想，主要原因是用户密码的取值空间过于庞大。

这里我们通过简单的计算，来对取值空间有一个更加直观的认识。一般用户密码的单字符可选范围是26个小写字母、26个大写字母、10个数字以及少数特殊字符，我们假设用户密码是8位（要知道8位密码并不算强度很高的设置），那么经过计算，密码合计取值范围就是72万亿。

单字符取值范围 ≈ 26 + 26 + 10 + 10 = 72

8个字符的密码取值空间 = 72 ^ 8 = 722204136308736 ≈ 72万亿

按照每秒能够计算100万个密码的散列值来计算，需要大约8358天，相当于22.9年才能完成密码空间的遍历，很显然这种攻击是无法真正实施的，因此暴力破解攻击无效。

722204136308736 / (1000000 * 3600 * 24) ≈ 8358

按照每个8位密码占据8个字节的存储空间来计算，72万亿的密码空间大约会占据5254TB的存储空间，很显然这种攻击也是无法真正实施的，因此字典攻击也是无效的。

722204136308736 * 8.0 / (1024 * 1024 * 1024 * 1024) ≈ 5254

综合上面的分析，我们可以发现，暴力破解没有空间占用但时间消耗过大，而字典攻击几乎没有时间占用但空间消耗过大。因此，为了有效地对散列值进行攻击，我们需要一种更可行的方案。在这种方案里，我们能够接受多一些的解密时间，但希望它不要占用过大的空间。目前，这种平衡了时间和空间的攻击方案就是彩虹表攻击。

彩虹表攻击

HASH链

以字典攻击为基础，通过算法设计来实现时间换取空间的效果，就是彩虹表攻击的原理。

彩虹表攻击中所涉及的算法就是预计算的HASH链。

为了实现预计算的HASH链，我们需要一个新型函数的辅助，一般会称之为归约函数或者约简函数。但是千万不要为这个名字感到困惑，它其实并没有真实地表达什么含义，你可以简单地理解为一个新函数R。R函数与HASH函数执行相反的运算流程，比如，HASH函数将原始输入映射到HASH散列值，而R函数则是将HASH散列值映射回原始输入，并且R函数的映射关系是可以任意指定的。

接下来我来带你实际构建一个HASH链，在这个过程中，你将对稍显复杂的彩虹表攻击有更直观的理解。

以MD5散列为例，首先我们随机选择一段明文talentsec并对其取md5散列，获得结果6f66114d09e7b9ddbfa8b286ea1e57a7，接下来我们按照自己的喜好定义一个R函数，并且使用R函数对散列值6f66114d09e7b9ddbfa8b286ea1e57a7进行运算，获得结果aaaaaaaaa。继续重复上述过程，即不断使用HASH函数和R函数进行计算，产生的如下链条就是HASH链：

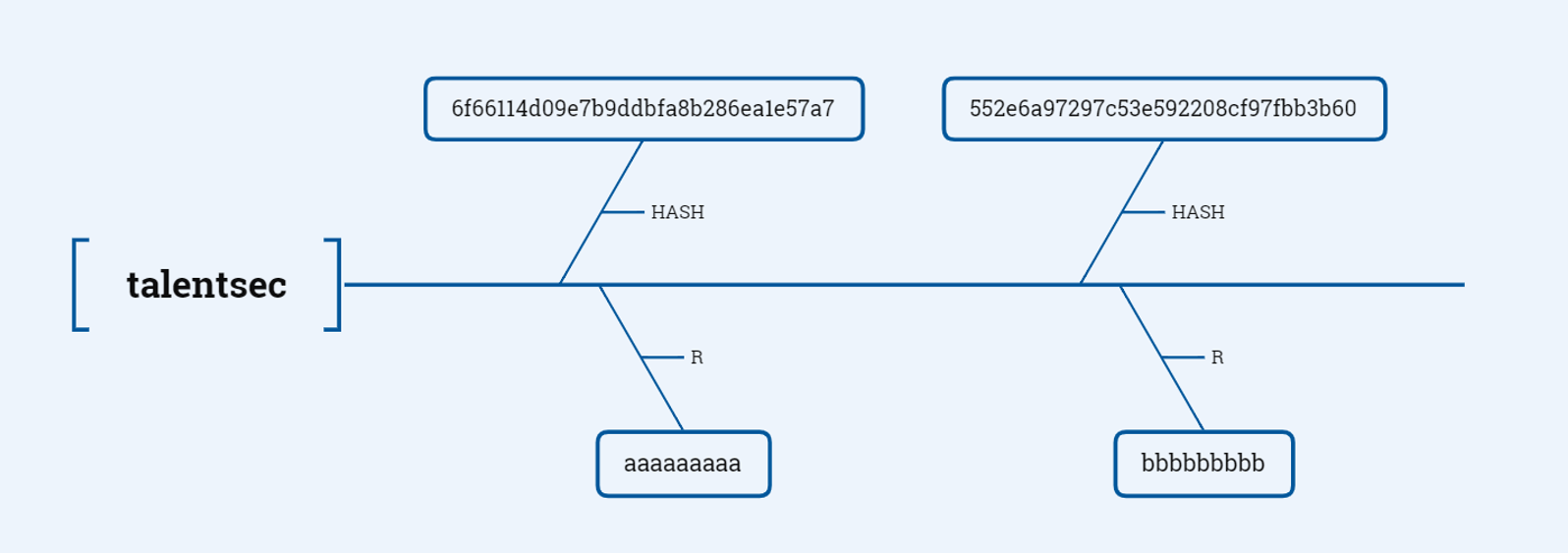
通过随机选择多段明文重复执行这个过程，会产生多个HASH链，这些HASH链我们称为预计算的HASH链集。需要注意的是，存储的过程中我们只需要保存HASH链的头和尾，对于上述示例HASH链，我们只进行了2轮计算，所以其存储形态应该是(talentsec,bbbbbbbbb)。

那么我们要如何使用预计算的HASH链来进行攻击呢？

作为攻击者，我们需要破解一个HASH散列值。通过对该散列值进行多轮次的R函数、HASH函数计算，我们可以取得多个原始输入，如果原始输入与HASH链的头或者尾产生碰撞，HASH散列值的破解结果则很有可能存在于该链条中。

这里我们通过2个场景示例来直接感受一下，对于上述场景，如果我们希望破解的散列值是552e6a97297c53e592208cf97fbb3b6，通过1次R函数可以获得原始输入bbbbbbbbb，成功匹配到HASH链(talentsec,bbbbbbbbb)，通过从头执行HASH链的计算过程，可以得出破解结果是aaaaaaaaa；同样是上述场景，如果我们希望破解的散列值是6f66114d09e7b9ddbfa8b286ea1e57a7，通过R函数-HASH函数-R函数计算可以获得原始输入bbbbbbbbb，依然成功匹配到HASH链(talentsec,bbbbbbbbb)，通过从头执行HASH链的计算过程，可以得出破解结果是talentsec。

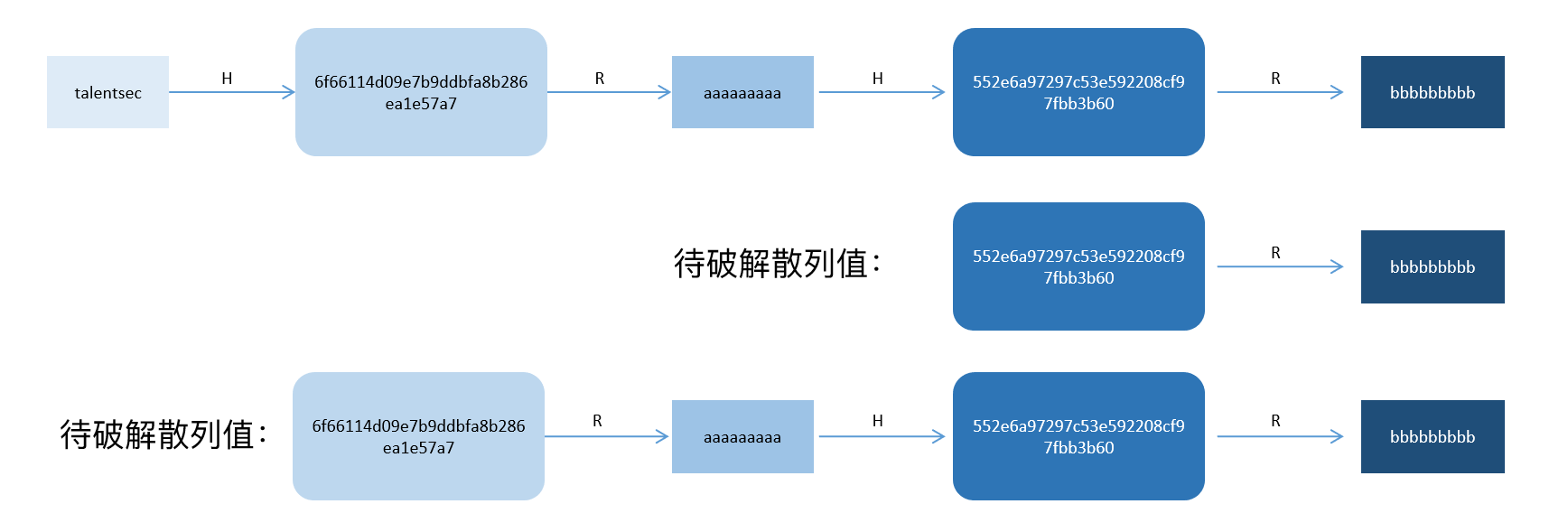
值得一提的是，破解中需要的运算轮次，一般与HASH链的计算轮次相同，如果达到了计算轮次却并未找到匹配的HASH链，则直接返回破解失败。

关于预计算HASH链的理想性能表现，我们可以通过简单的计算来分析。依然是8位密码的情况，假设我们定义了一个R函数，让每条HASH链能够执行1亿次计算，那么完成HASH链集的存储只需要大约220MB的空间。

722204136308736 / 50000000 ≈ 14444082 条HASH链

722204136308736 * 16 / (50000000 * 1024 * 1024) ≈ 220 MB

依然按照每秒100万次的速度来计算，单一HASH散列值从生成一条新的HASH链到完成匹配的时间预计不超过2分钟。

100000000 / (1000000 * 60) ≈ 1.67 mins

彩虹表

那么，预计算的HASH链集就是彩虹表吗？其实并非如此。

预计算的HASH链集仍然存在着一些不足，主要是在性能表现方面。我们刚刚计算的攻击时间都是在理想情况下推演出来的，但是未经优秀设计就生成的预计算HASH链集，实际上并不能达到这个性能水平，因此才会出现彩虹表。我们可以将彩虹表理解为是一种经过精密设计的预计算HASH链集，在攻击时能发挥出理想的性能表现。

那么预计算HASH链集需要优化的核心点是哪里呢？接下来我们就一起来分析一下。

通过前面我们所讨论的攻击过程，不难判断，预计算的HASH链集包含多条HASH链，这一点我们从它的名字也不难看出，而每条HASH链能够覆盖的攻击范围，与它执行的计算次数呈现线性相关。最理想的情况当然是，每条HASH链所覆盖的攻击范围彼此互斥，这样在n条链的情况下，覆盖的攻击范围就是n x 单链计算次数/2。但现实往往没有这么理想，R函数的选择与设计可能会导致碰撞情况的发生：

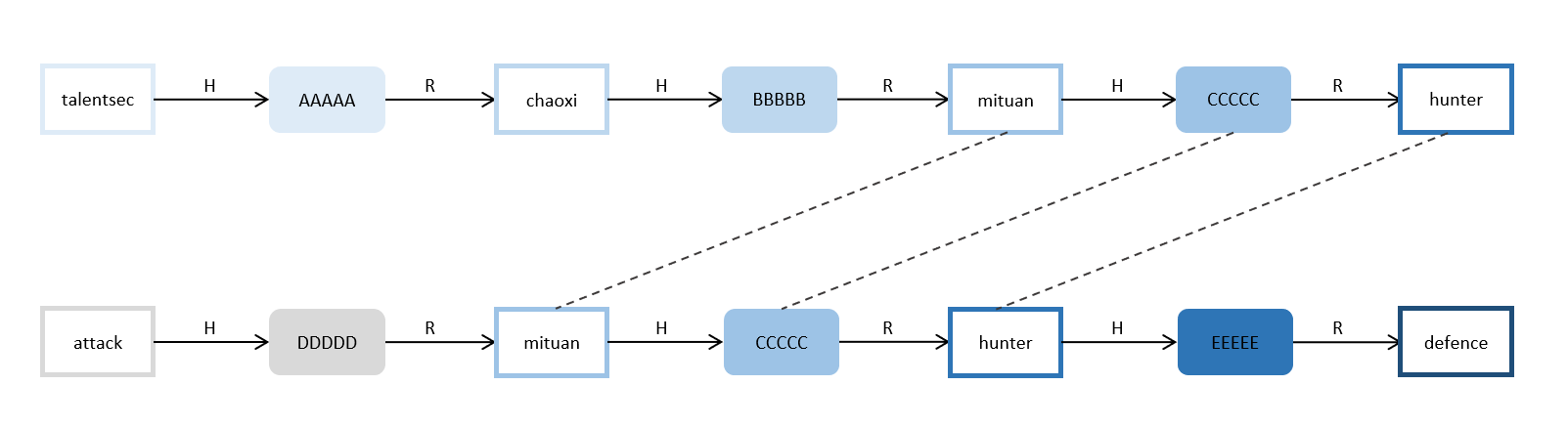
通过上述示例可以发现，存在设计缺陷的R函数会导致大量碰撞的发生，而一旦中间某节点发生碰撞，就会导致后续节点全部碰撞，这样会大大缩小预计算HASH链集能够覆盖的攻击范围。又因为预计算HASH链只保存收尾节点，因此想要发现两条链的高度相似性是非常难的。

彩虹表的出现正是为了解决R函数引起的链碰撞问题。

彩虹表的设计理念是，在生成预计算的HASH链时采用多种R函数，也就是在每个轮次的计算中分别使用R1、R2、R3函数等，大致含义如下：

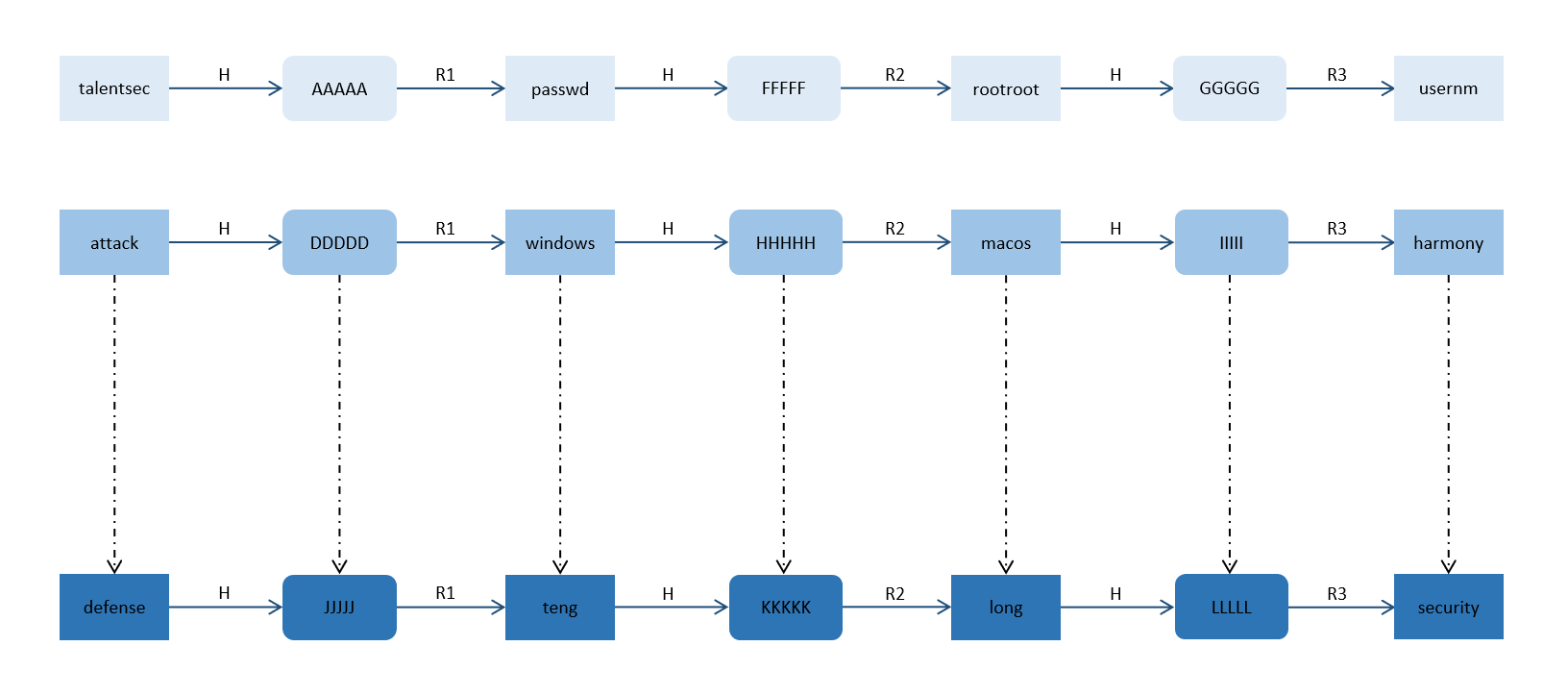
这样即使发生了之前我们所描述的碰撞情况，通常会是以下这种情况：

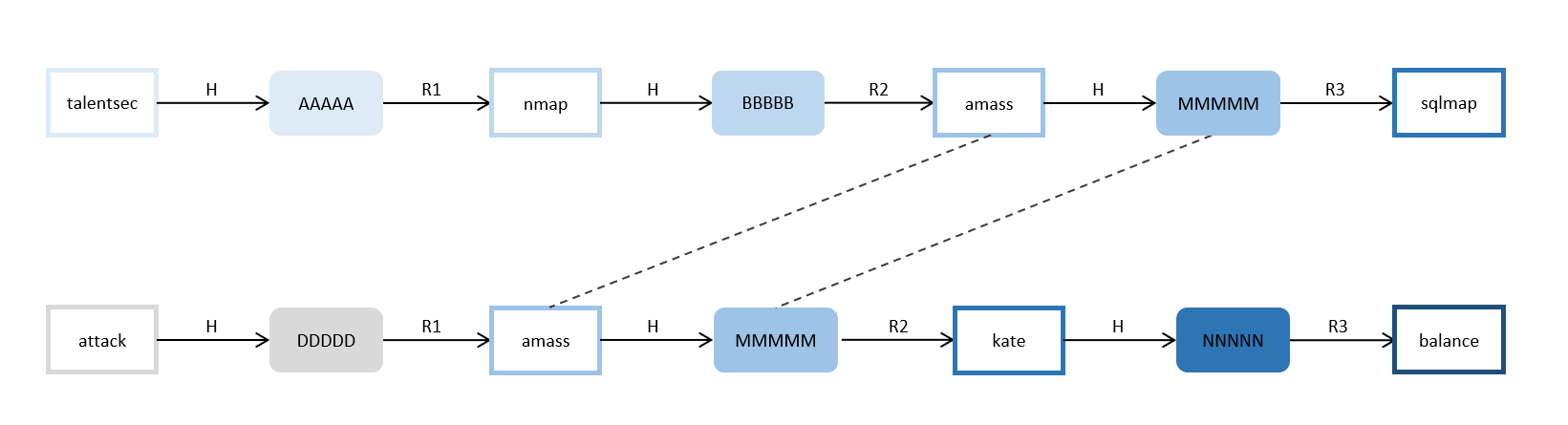
可以看到，虽然部分节点发生了碰撞，但是由于发生碰撞的位置并非在同一序列，使用的R函数也不是同一个，因此后续产生的节点也不相同。

这样，即使同一序列位置发生碰撞，导致后续节点完全相同，但是因为末节点是相同的，所以我们仍然可以非常快速地找出这条相似链，删除它来优化存储空间。

而关于彩虹表的使用方法，本质上与HASH链集并无二致，核心思想仍然是计算得出R函数的结果并与HASH链进行匹配。它们的区别在于，计算出的序列结果是否唯一。因为HASH链集使用的是相同的R函数，所以，如果我们对待破解的HASH散列进行R函数计算，所产生的序列结果是唯一的；但是彩虹表使用的是不同的R函数，因此计算时需要将待破解的HASH散列带入不同位置，从而得出多个序列结果。